Binary logic deals with variables that take on two discrete values, which we often represent with 1s and 0s, true and false etc.
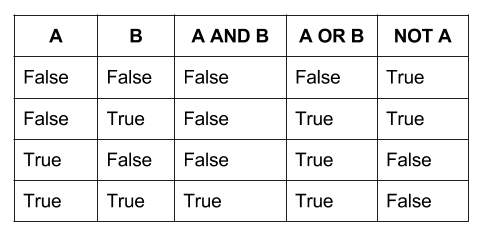
NOT: represented by a prime or an overbar, it is a unary operator which turns a 1 to a 0, and vice versa
AND: represented by a dot or the absence of an operator, it is a binary operator which results in a 1 only when both of its operands are 1, else it results in a 0.
OR: represented by a plus sign, it is a binary operator which results in a 0 only when both of its operands are 0, else it results in a 1.
Below we have the truth tables for these basic operations:

A binary operator defined on a set $S$ of elements is a rule that assigns, to each pair of elements from S, a single element from S.
The basic operations NOT, AND, OR are closed, and AND and OR are associative, and commutative in nature. The operator AND is distributive over OR, i.e. $x.(y + z) = (x.y) + (x.z)$, and the operator OR is distributive over AND, i.e. $x + y.z = (x + y).(x + z)$
In boolean algebra, proofs by truth table are valid, essentially being an exhaustive case analysis.
The duality principle and states that every algebraic expression deducible from the postulates of boolean algebra remains valid